Rocket engine nozzle
Rocket engine nozzle
Rockets use nozzles to accelerate hot exhaust to produce thrust as described by Newton’s third law of motion. The amount of thrust which is produced by the engine depends on the mass flow rate through the engine, the exit velocity of the flow, and the pressure at the exit of the engine. The values of these three flow variables are all determined by the design of the nozzle.
A nozzle is a device, which is shaped into tube through which hot gases flow. Rockets nozzle designs typically consist of a fixed convergent section followed by a fixed divergent section. The nozzle configuration is then called a convergent-divergent, or CD, nozzle. In a CD nozzle, the hot exhaust leaves the combustion chamber and converges down to the minimum area, or throat, of the nozzle.
The throat size is chosen to choke the flow and set the mass flow rate through the system. The flow in the throat is sonic which means the Mach number is equal to one in the middle of the throat. Downstream of the throat, the geometry diverges, and the flow is isentropically expanded to a supersonic Mach number that depends on the area ratio of the exit to the throat, Mach number is greater than 1.
Expansion of a supersonic flow causes that static pressure and temperature both decreases from the throat to the exit. The amount of the expansion determines the exit pressure and temperature. The exit temperature determines the exit speed of sound, which determines the exit velocity. The exit velocity, pressure, and mass flow through the nozzle determine the amount of thrust produced by the nozzle.
A rocket engine nozzle is a propelling nozzle, usually of the de Laval type, used in a rocket engine to expand and accelerate combustion products to high supersonic velocities.
 |
| A de Laval nozzle, showing approximate flow velocity increasing from green to red in the direction of flow; source: wiki |
Atmospheric use
The optimal size of a rocket engine nozzle is achieved when the exit pressure equals ambient (atmospheric) pressure, which decreases with increasing altitude.
If ambient pressure is higher than the exit pressure, it decreases the net thrust produced by the rocket, which can be seen through a force-balance analysis.
If ambient pressure is lower, while the force balance indicates that the thrust will increase, the isentropic Mach relations show that the area ratio of the nozzle could have been greater, which would result in a higher exit velocity of the propellant, increasing thrust. For rockets traveling from the Earth to orbit, a simple nozzle design is only optimal at one altitude, losing efficiency and wasting fuel at other altitudes.
 |
| Density flow in a nozzle; source: wiki |
Vacuum use
For nozzles that are used in vacuum or at very high altitude, it is impossible to match the ambient pressure. Nozzles with larger area ratio are usually more efficient. However, a very long nozzle has significant mass, which is disadvantage. Additionally, as the temperature of the gas in the nozzle decreases, some components of the exhaust gases, such as water vapor from the combustion process, may condense or even freeze. This needs to be avoided.
A de Laval nozzle
A de Laval nozzle (or convergent-divergent nozzle, CD nozzle or con-di nozzle) is a tube which is pinched in the middle, making a carefully balanced, asymmetric hourglass shape. It is used to accelerate a compressible fluid to supersonic speeds in the axial (thrust) direction, by converting the thermal energy of the flow into kinetic energy. De Laval nozzles are widely used in some types of steam turbines and rocket engine nozzles. It also sees use in supersonic jet engines.
Similar flow properties have been applied to jet streams within astrophysics.
 |
| Diagram of a de Laval nozzle, showing approximate flow velocity (v), together with the effect on temperature (T) and pressure (p); source: wiki |
de Laval nozzle in 1 dimension
- The combustion gas is assumed to be an ideal gas.
- The gas flow is isentropic; i.e., at constant entropy, as the result of the assumption of non-viscous fluid, and adiabatic process.
- The gas flow rate is constant (i.e., steady) during the period of the propellant burn.
- The gas flow is non-turbulent and axisymmetric from gas inlet to exhaust gas exit (i.e., along the nozzle's axis of symmetry).
- The flow is compressible as the fluid is a gas.
 |
| Nozzle Types; source: Расчёт сопел современных ракетных двигателей / Хабр (habr.com) |
 |
Figure above: Nozzles can be (top to bottom):
- underexpanded
- ambient
- overexpanded
- grossly overexpanded.
If a nozzle is under- or overexpanded, then loss of efficiency occurs relative to an ideal nozzle. Grossly overexpanded nozzles have improved efficiency relative to an underexpanded nozzle (though are still less efficient than a nozzle with the ideal expansion ratio), however the exhaust jet is unstable.
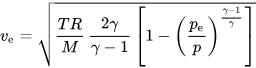

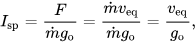




Comments
Post a Comment